puntos de inflexión

 puntos de inflexión

son aquellos en los que la función pasa de cóncava a convexa o de convexa a cóncava. Matemáticamente esto ocurre cuando la segunda derivada de la función en el punto considerado cambia de signo, y además la función f está definida en el punto considerado.

Punto de inflexión

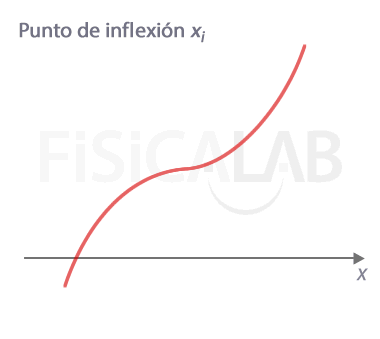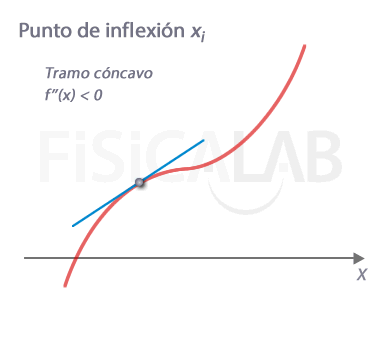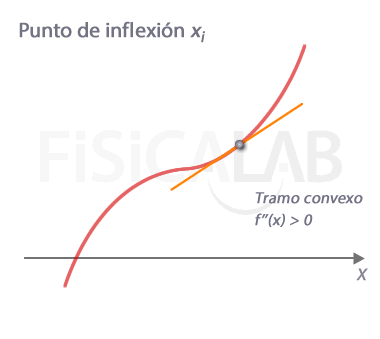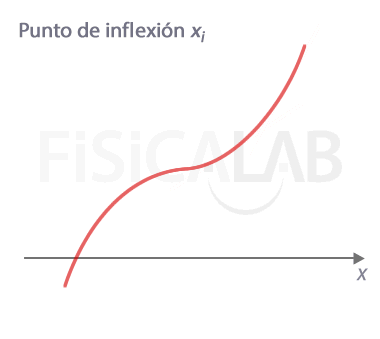
En x=xi tenemos un punto en el que cambia la curvatura de la función. Es por tanto un punto de infléxión. Observa que en él la recta tangente queda por encima de la función en un lado, y por debajo en otro, es decir, la "atraviesa". Además, el signo de la segunda derivada es diferente a la izquierda y a la derecha del punto, siendo f''(xi)=0.

¿Por qué f''(xi)=0?

Como hemos indicado, partimos de la premisa de que la segunda derivada es continua en xi. Para que haya un cambio de curvatura se debe cumplir que en cualquier entorno de xi la segunda derivada tenga signos distintos. Debido a la continuidad de f'' esto implica necesariamente que en el propio punto debe ser 0, es decir, f''(xi)=0.

Esta condición, aunque necesaria, no es suficiente, de ahí que también sea necesario que f'''(xi)≠0

Punto de inflexión y segunda derivada

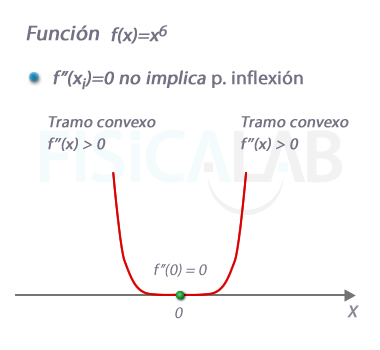
La función f(x)=x6 representada en la figura cumple que f''(0)=0, sin embargo puedes ver que en x=0 no cambia su curvatura (que es la misma en todo su dominio). Así, el signo de f'' es el mismo en ambos lados de 0.